857. Выпуклая оболочка
На плоскости
заданы n точек своими декартовыми
координатами. Найти минимальный периметр многоугольника, содержащего все эти
точки. Гарантируется, что искомый многоугольник имеет ненулевую площадь.
Вход. Первая строка содержит количество точек n (3 ≤ n ≤ 1000) на плоскости. Далее следуют n строк, каждая из которых содержит пару координат xi, yi (-10000 ≤ xi,
yi ≤ 10000). Все
числа целые, все точки различны.
Выход. Вывести длину
периметра искомого многоугольника с одним знаком после запятой.
|
Пример
входа |
Пример
выхода |
|
5 1 0 0 1 -1 0 0 -1 0 0 |
5.7 |
РЕШЕНИЕ
геометрия
– выпуклая оболочка
Анализ алгоритма
Искомый многоугольник представляет собой выпуклую оболочку заданного
множества точек. Ее будем искать обходом Грэхема.
Пример
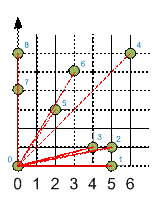
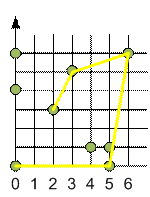
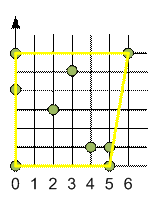
Рассмотрим процесс построения выпуклой оболочки.
Самая левая
точка (0, 0) находится в центре. В ней будет начинаться и заканчиваться
построение выпуклой оболочки. На рисунке справа приведена сортировка точек по
полярному углу. Точки (0, 0) и (5, 0) обязательно принадлежат выпуклой
оболочке.




Реализация алгоритма
Объявим класс
точка и операторы их сложения и вычитания.
class Point
{
public:
int x, y;
Point(int x =
0, int y = 0)
{
this->x
= x; this->y = y;
}
double len2()
const {return
x*x + y*y;}
};
Point operator+ (Point a, Point b)
{
return
Point(a.x+b.x,a.y+b.y);
}
Point operator- (Point a, Point b)
{
return
Point(a.x-b.x,a.y-b.y);
}
Функция PolarAngle возвращает полярный угол точки p в промежутке [-PI; PI].
double PolarAngle(Point p)
{
return
atan2(1.0*p.y,1.0*p.x);
}
Функция сортировки точек по полярному
углу. Если две точки a и b имеют одинаковый полярный угол, то
сортируем их по увеличению расстояния от начала координат.
int f(Point a, Point b)
{
if
(fabs(PolarAngle(a) - PolarAngle(b)) < EPS)
return
a.len2() < b.len2();
return
PolarAngle(a) < PolarAngle(b);
}
Функция TurnLeft возвращает истину, если точки a, b и c образуют левый поворот.
int TurnLeft(Point a, Point b, Point c)
{
Point q = b - a, w = c - b;
return q.x *
w.y - w.x * q.y > EPS;
}
Основная часть программы. Читаем в вектор пар v координаты
входных n точек.
scanf("%d",&n);
for(i = 0; i < n; i++)
{
scanf("%d
%d",&a,&b);
v.push_back(Point(a,b));
}
Ищем самую левую точку (точку с
наименьшей x координатой). Если таких
точек несколько, то берем нижнюю точку (точку с наименьшей y координатой). Занесем эту точку в v[0]. Она однозначно будет
лежать на выпуклой оболочке.
for(i = 1; i < n; i++)
{
if (v[i].x
< v[0].x) swap(v[i],v[0]);
if ((v[i].x
== v[0].x) && (v[i].y < v[0].y)) swap(v[i],v[0]);
}
Совершим параллельный перенос осей
координат так, чтобы точка v[0] стала центром. Отнимаем изо всех точек точку Center = v[0].
Center = v[0];
for(i = 0; i < n; i++) v[i] = v[i] -
Center;
Сортируем все точки, кроме начальной,
по полярному углу. Добавим в конец первую (центральную) точку.
sort(v.begin()+1,v.end(),f); v.push_back(v[0]); n++;
Запускаем обход Грэхема. Все точки от
v[0] до v[cur] образуют выпуклую
оболочку. Рассмотрим очередную точку v[i].
Если точки v[cur – 1], v[cur] и v[i] не образуют левую тройку, то v[cur] не будет принадлежать выпуклой оболочке. Производим в цикле
выталкивание таких точек v[cur],
после чего заносим v[i] в выпуклую
оболочку.
for(cur = 1, i = 2; i < n; i++)
{
while( (cur
> 0) && !TurnLeft(v[cur-1],v[cur],v[i])) cur--;
v[++cur] = v[i];
}
Возвращаем прежние координаты точкам.
for(i = 0; i <= cur; i++) v[i] = v[i]
+ Center;
Вычисляем периметр многоугольника, являющегося
выпуклой оболочкой.
for(i = 0; i < cur; i++)
p += sqrt(1.0*(v[i+1] - v[i]).len2());
Выводим значение периметра p.
printf("%.1lf\n",p);
Реализация алгоритма –
сортировка точек через направление поворота
#include <cstdio>
#include <vector>
#include <algorithm>
#include <cmath>
using namespace std;
class Point
{
public:
int x, y;
Point(int x = 0, int y = 0)
{
this->x = x; this->y
= y;
}
double len2() const {return x*x + y*y;}
};
Point operator+ (Point a,
Point b)
{
return Point(a.x+b.x,a.y+b.y);
}
Point operator- (Point a,
Point b)
{
return Point(a.x-b.x,a.y-b.y);
}
vector<Point> v, hull;
int i, n, cur, a, b;
double p;
int TurnLeft(Point a, Point b, Point c)
{
Point p = b - a, q = c - b;
return p.x *
q.y > q.x * p.y;
}
Сортируем точки по возрастанию
полярного угла относительно центральной v[0]. Точка b имеет больший полярный угол чем а (то есть a < b), если поворот (v[0], a, b)
является левым. Если все три точки v[0], a,
b коллинеарны, то a < b если только расстояние от начала координат до a меньше чем до b. В случае правого поворота (v[0], a, b) компаратор f должен
вернуть 0.
int f(Point a, Point b)
{
Point p = a - v[0], q = b - a;
if(p.x * q.y
== q.x * p.y)
return
a.len2() < b.len2();
return p.x *
q.y > q.x * p.y;
}
Еще один вариант реализации функции
сортировки. Вычтем из точек a и b точку v[0], получив векторы a
и b. Совместим начало вектора b с концом a.
Если векторы a и b образуют левый поворот, то полярный
угол исходной точки a меньше
полярного угла исходной точки b (a < b).
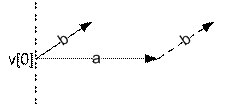
Если векторы a и b коллинеарны, то ближе к v[0] будет конец более короткого
вектора.
int f(Point a, Point b)
{
a = a - v[0]; b = b - v[0];
if(a.x * b.y
== b.x * a.y)
return
a.len2() < b.len2();
return a.x *
b.y > b.x * a.y;
}
int main(void)
{
scanf("%d",&n);
for(i = 0; i < n; i++)
{
scanf("%d %d",&a,&b);
v.push_back(Point(a,b));
}
for(i = 1; i < n; i++)
{
if (v[i].x < v[0].x) swap(v[i],v[0]);
if ((v[i].x == v[0].x) && (v[i].y <
v[0].y)) swap(v[i],v[0]);
}
sort(v.begin()+1,v.end(),f);
v.push_back(v[0]); n++;
v[0]
содержит самую левую нижнюю точку. Параллельный перенос координат (так чтобы
v[0] стало центром координат) можно не делать.
for(cur = 1, i = 2; i < n; i++)
{
while( (cur > 0) &&
!TurnLeft(v[cur-1],v[cur],v[i])) cur--;
v[++cur] = v[i];
}
for(i = 0; i < cur; i++)
p +=
sqrt(1.0*(v[i+1] - v[i]).len2());
printf("%.1lf\n",p);
return 0;
}